Dynamics of Tropical Instability Vortices

Background

Tropical instability waves (TIWs) are cusp-like perturbations that form on the sea surface temperature fronts either side of the eastern Pacific cold tongue in the equatorial Pacific. They form through a combination of barotropic instability acting on the lateral shears of the zonal current system and baroclinic instability acting on the equatorial fronts. They have been studied extensively to determine their formation mechanisms, large-scale fluxes and influences on processes such as ENSO.

Tropical instability vortices form to the north of the equator when TIWs become strong enough to go nonlinear and form coherent anti-cyclonic vortices of radius ~ 500km. Due to their energetic circulation, strong anticyclonic vorticity and location close to the equator, the water forming the core of the TIV is characterized by a Rossby number of order -1. Therefore, the core water is also characterised by small values of the Ertel potential vorticity (PV):

$q=(f+\zeta)N^2+\omega_h\cdot\nabla_h b=q_v+q_h$

where $\zeta$ is the vertical component of the relative vorticity, b is the buoyancy, $N^2$ is the vertical buoyancy gradient or stratification, $\omega_h$ is the horizontal vorticity and $\nabla_h b$ is the horizontal buoyancy gradient. The potential vorticity q is conserved along fluid parcels in the absence of friction and diabatic processes. The potential vorticity is particularly important because knowledge of its spatial and temporal distribution allows determination of the entire balanced flow field, through the concept of PV inversion ( Hoskins et al. (1985) QJRMS , 111(470): 877-946). The PV has been split into two terms, one associated with the vertical vorticity and one associated with the horizontal vorticity and horizontal buoyancy gradients. This second baroclinic term can be large at strong submesoscale fronts in the midlatitudes, where the horizontal buoyancy gradient and thermal wind shear are large. We have also found that it is important in the formation of TIV core water (see below), highlighting the similarities between TIV dynamics and submesoscale dynamics in the midlatitudes.

TIV core water and TIV driven lateral mixing

Where does the low PV water that forms the core of the TIVs come from? Since the Coriolis parameter changes sign at the equator, one possibility is that it is formed from Southern Hemisphere water advected over the equator. Other possibilities are that the PV is locally lowered before and during its entrance into the tropical instability vortices through frictional processes (down-front winds) or diabatic processes (surface cooling).

The image below shows a set of Lagrangian floats at times two months apart in a ROMS simulation of the Equatorial Pacific Ocean. At the initial time the floats are located mainly along the Equator (in the Equatorial Undercurrent (EUC)) with a small number located more to the north in the North Equatorial Counter Current (NECC). Two months later all the floats have entered a TIV. The floats experience significant Lagrangian changes in temperature and salinity, showing that the TIVs homogenise T-S properties and drive significant lateral mixing. This TIV driven lateral mixing across the North Equatorial Front can warm the Equatorial Cold Tongue and thus influence processes of global climate importance such as the El Nino - Southern Oscillation.

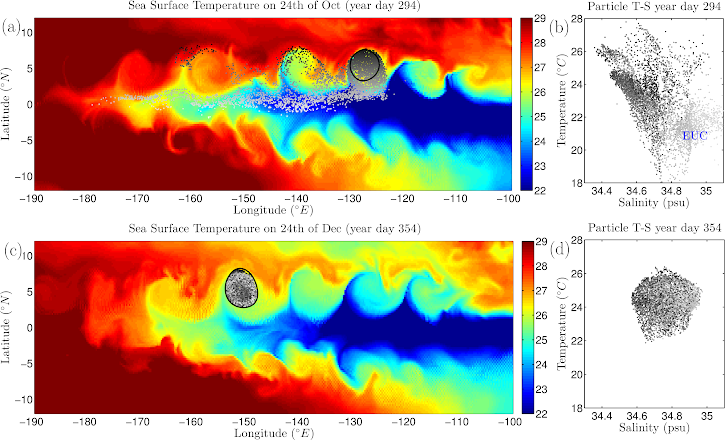
SST and Floats

Figure 1: (a) Model SST and Lagrangian particle positions on 24th of October. (c) Model SST and Lagrangian particle positions two months later once the particles have entered a TIV. (b), (d) corresponding T-S diagrams over the floats showing that TIVs homogenise T-S and mix water masses together.

TIV core water formation

In my paper published in the Journal of Physical Oceanography (Potential Vorticity Dynamics of Tropical Instability Vortices), I investigated the mechanisms through which the strong anticyclonic (clockwise in the Northern Hemisphere) vorticity of TIVs is formed. By studying the vorticity and buoyancy equations along Lagrangian fluid parcel tracks I was able to show that several processes contribute to the creation of TIV anticyclonic vorticity. Rearranging the equation for the PV above and normalizing by a mean $\overline{N^2}=1.6\times10^{-4}s^{-2}$ and mean $\overline{f}=1.27\times10^{-5}s^{-1}$ appropriate for the vortex center at 5N gives;

$\frac{\Delta\zeta}{\overline{f}}=-\frac{\Delta f}{\overline{f}} + \frac{\Delta q}{\overline{f}\overline{N^2}}-\frac{\Delta q_h}{\overline{f}\overline{N^2}} - \frac{(\overline{f}+\overline{\zeta})\Delta N^2}{\overline{f}\overline{N^2}}$

Showing that changes in the relative vorticity $\Delta\zeta$ can be driven by advection of planetary vorticity $\Delta f$ , changes in the baroclinic term in the PV $\Delta q_h$ , changes in the stratification $\Delta N^2$ or non-conservative changes in the total PV $\Delta q$ . The dominant contribution to the creation of anticyclonic vorticity for TIVs turns out to be the advection of planetary vorticity term. However, the baroclinic term involving also makes a significant contribution through the mechanism of baroclinically-low to votically-low PV conversion and vortex tilting. This mechanism is summarised in the following schematic:

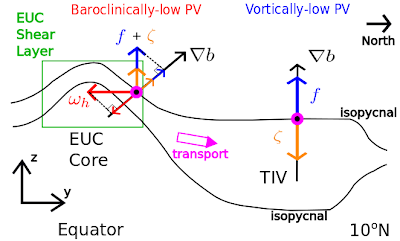
PV Schematic

Figure 2: A schematic showing the mechanism of baroclinically-low to vortically-low PV conversion and how it leads to the formation of strong anticyclonic vorticity within a TIV core.

This mechanism is also involved in the formation of so called intrathermocline eddies (ITEs) with scales of some 10’s of kilometers in the midlatitudes. Thus we have shown that there are similarities between midlatitude submesoscale physics and larger-scale flows at the Equator, similarities that can be exploited to understand some aspects of equatorial dynamics.

Dr Ryan Holmes

Background

TIV core water and TIV driven lateral mixing

TIV core water formation