Polymer Physics
My honours year research project at ANU was in computational polymer physics where I worked with Professor David Williams. I also worked as a research assistant for six months in this field, publishing two papers in Macromolecules and Europhysics letters
Background
Polymers
A polymer consists of a long chain of repeating structural units called monomers. A typical monomer would be an ethylene molecule (C2H4) in the case of the polymer polyethylene. By combining different combinations of monomers and chains of different architectures (single chains, star chains, bottle brushes, networks) a variety of useful materials can be formed, such as plastics, rubbers, clothing and nano-particles. Polymers also occur naturally, with some biological examples being DNA, RNA, and proteins. Due to their usefulness in building materials, and their ubiquity in nature, the understanding of how different polymer chains behave in different environments is important and the subject of much modern research. Unsolved problems include the protein folding problem and the construction of nano-particles out of polymers.
The physics of block copolymers in poor solvents
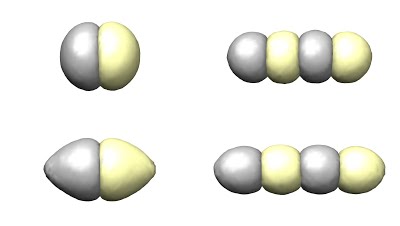
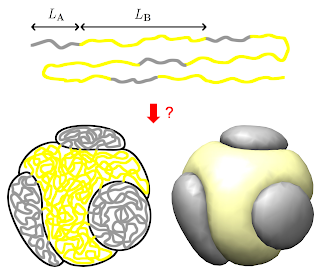
My work involved trying to understand the behavior of single chain block copolymers in poor solvents using self-consistent field theory simulations and theoretical free-energy models. A single chain block copolymer is a linear polymer chain with two different types of monomers arranged in continuous blocks (upper drawing). A poor solvent is a solvent (such as water), that the polymer does not like being in contact with. Thus when placed in a poor solvent, the polymer collapses into a tight ball in order to minimize the solvent-polymer contact area. In addition, the two different monomer species in the chain do not like contact with each-other, and thus they attempt to separate into separate domains within the larger collapsed polymer ball. A competition exists between the minimization of polymer-solvent surface area, polymer species-to-species surface area and the maintenance of the connectivity of the polymer chain. The result of this competition determines the polymer conformation (shape/geometry) that minimizes the free-energy, and thus the equilibrium shape of the polymer (lower drawing). Thus by changing parameters such as the polymer chain block lengths, solvent strength and species repulsion strength, the final conformation of the polymer can be controlled.
Self-consistent field theory
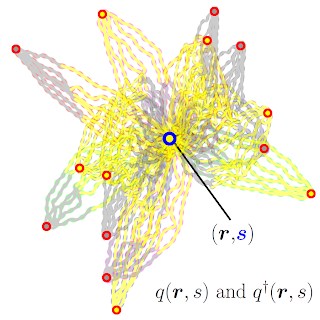
I wrote a self-consistent field theory simulation in FORTRAN for simulation of the collapsed conformation of a given polymer chain and interaction strengths. Self-consistent field theory simulations (SCFT) are similar in a sense to Monte-Carlo simulations, where changes are made in a given conformation and kept or eliminated depending on changes in the free-energy of the total conformation. However, in SCFT, the individual monomers are abstracted to probabilistic density fields. The goal of the SCFT simulation is then to find the density fields of each polymer species (A and B for a copolymer with two species) that minimizes the free-energy. This process is performed iteratively using the mathematical construct of a propagator to maintain the connectivity of the polymer chain despite the abstract density fields. The final conformations obtained are estimates of the average lowest free energy conformation of the polymer (and sometimes, as I identified, they can be unphysical due to the averaging process).
Theoretical Free-energy modeling
In addition to the self-consistent field theory simulations, I also used some theoretical free-energy models of my polymers to confirm and compare against the simulations. These models consist of modeling the final polymer conformations in terms of geometrical shapes and using simple theoretical formulas of the free-energy due to certain areas of polymer-solvent surface contact and polymer-polymer contact. The total free-energy of the conformation can then be minimized with respect to geometrical free parameters to give a prediction of the lowest-energy conformation.
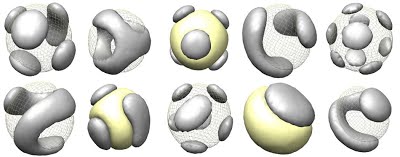
Block Copolymers as Patchy Colloids
My honours thesis was on The Morphology of Single Chain Asymmetric Block Copolymers in Poor Solvents. In this thesis, I focused on block copolymers where the blocks of one species were much longer than the blocks of other species. In this thesis and accompanying paper in Macromolecules, I showed that this class of polymers collapse into conformations consisting of a series of small balls of one species on the surface of a large sphere of the other species. This conformation is similar to nano-particles called patchy colloids, which are useful as they can assemble into materials such as optical lattices. However, patchy colloid like particles formed from block-copolymers would be smaller than conventional patchy colloids and thus could be extremely useful for forming the same structures at a different scale. Using both my SCFT simulations and theoretical free-energy scaling models, I was able to determine the number of patches formed for a range of polymer and solvent parameters. Thus my work could be used to determine what polymer chains must be constructed to give a desired nano-particle.
Conformation Transitions in Stretched Block Copolymers
In a second paper I explored the physics of stretched block copolymers. It is possible using certain grafting techniques to stretch a linear polymer chain by increasing the distance between the two end points. For block copolymers, certain interesting and sudden transitions can occur as the chain elongation is increased. In this paper I examined a simple four block copolymer and identified a transition where the unstreched conformation containing two domains would split into four domains. I was able to identify the elongation distance at which this transition occurs as a function of the parameters of the solvent and polymer. This prediction was confirmed using a theoretical free-energy scaling model.